On the clique number of noisy random geometric graphs
Type:
Papers
Publisher:
Random Structures & Algorithms
Submitted:
Oct 2022
Accepted:
Oct 2022
Publication date:
2023
Abstract:
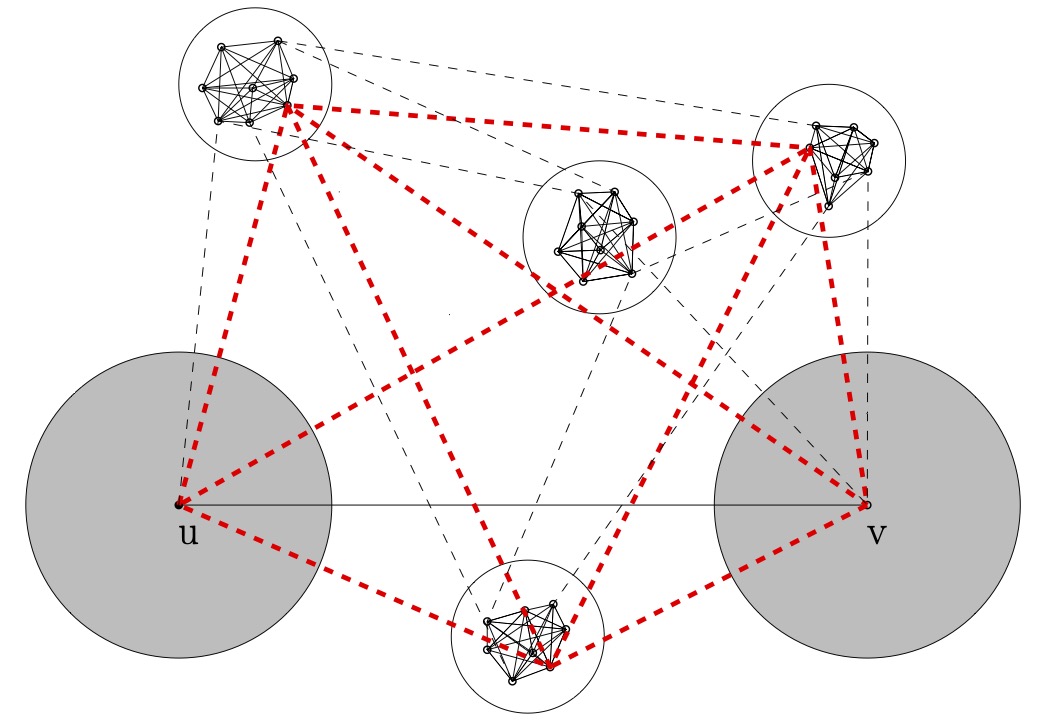
Let $G_n$ be a random geometric graph, and then for $\pp,\qqq \in [0,1)$ we construct a \emph{$(\pp,\qqq)$-perturbed noisy random geometric graph} $G_n^{\pp,\qqq}$ where each existing edge in $G_n$ is removed with probability $\pp$, while and each non-existent edge in $G_n$ is inserted with probability $\qqq$. We give asymptotically tight bounds on the clique number $\omega\left(G_n^{\pp,\qqq}\right)$ for several regimes of parameter.
External link:
