Warmth and mobility of random graphs

////////////////////////////////////////////

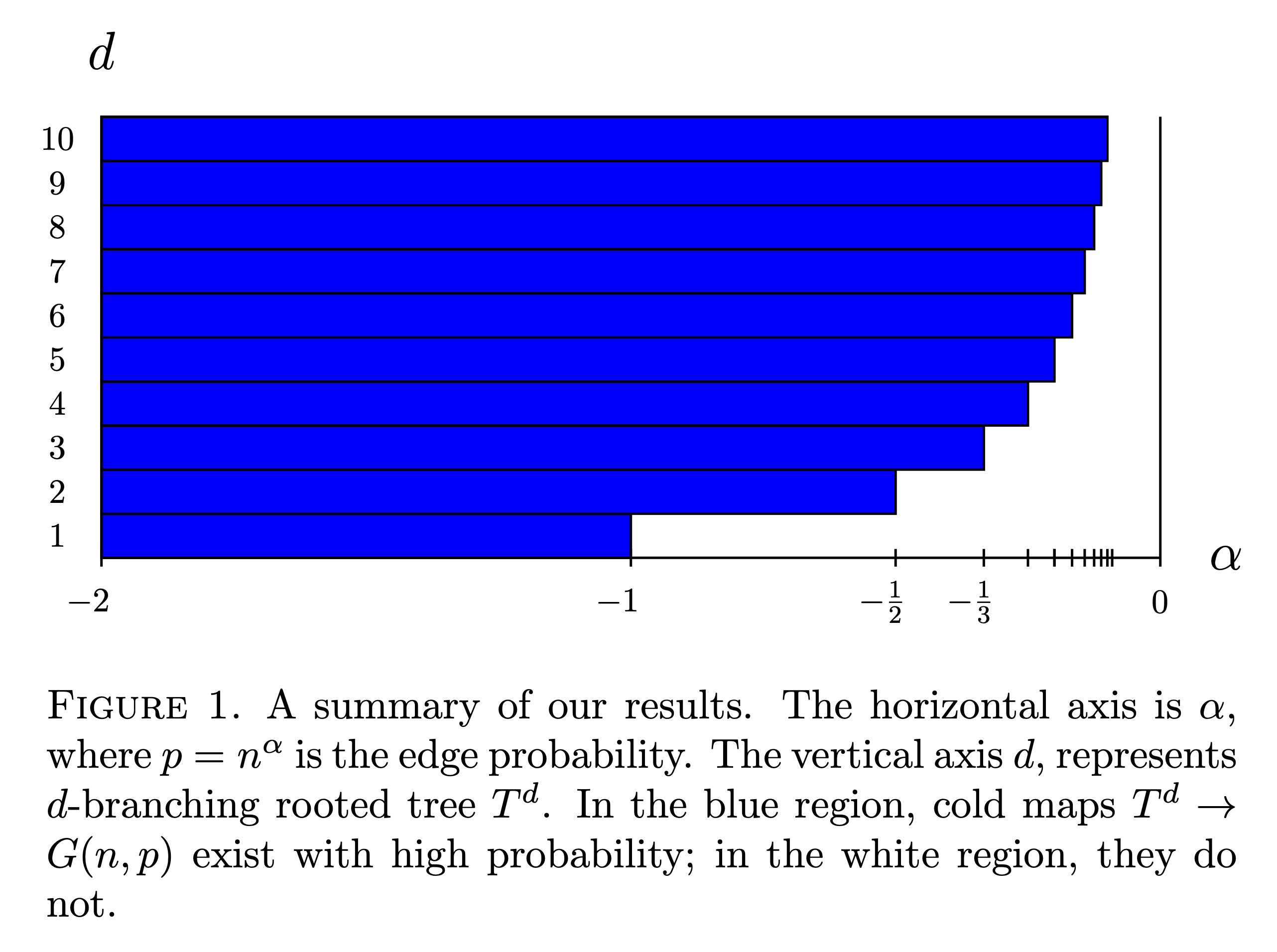
A graph homomorphism from the rooted $d$-branching tree $\phi: T^d \to H$ is said to be cold if the values of $\phi$ for vertices arbitrarily far away from the root can restrict the value of $\phi$ at the root. Warmth is a graph parameter that measures the non-existence of cold maps. We study warmth of random graphs $G(n,p)$, and for every $d \ge 1$, we exhibit a nearly-sharp threshold for the existence of cold maps. As a corollary, for $p=O(n^{-\alpha})$ warmth of $G(n,p)$ is concentrated on at most two values. As another corollary, a conjecture of Lovász relating mobility to chromatic number holds for ``almost all'' graphs. Finally, our results suggest new conjectures relating graph parameters from statistical physics with graph parameters from equivariant topology.