Homology of configuration spaces of hard squares in a rectangle

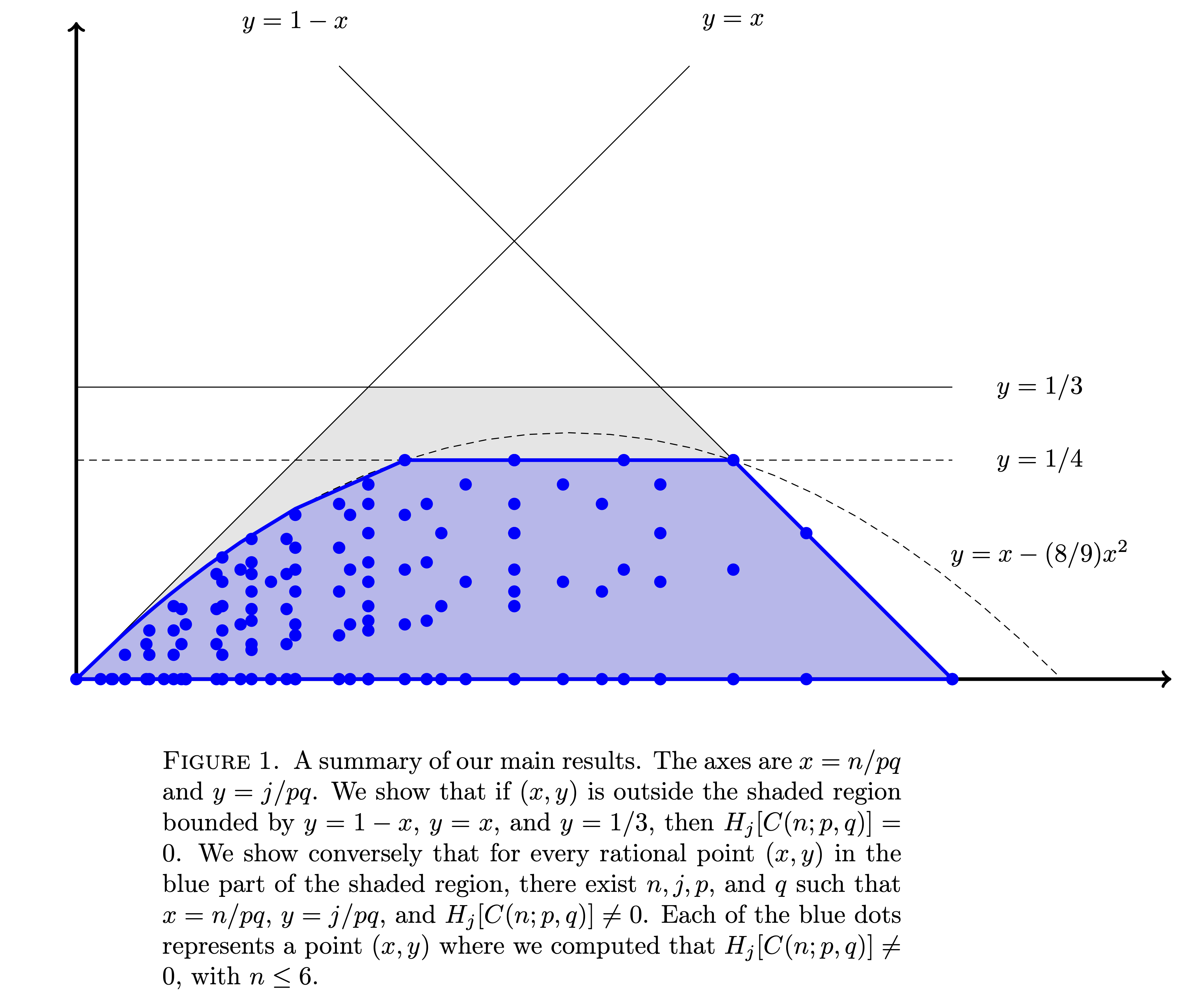
We study the configuration spaces $C(n,p,q)$ of $n$ labeled hard squares in a $p \times q$ rectangle, a generalization of the well-known ``15 Puzzle''. Our main interest is in the topology of these spaces. Our first result is to describe a cubical cell complex and prove that is homotopy equivalent to the configuration space. We then focus on determining for which $n$, $j$, $p$, and $q$ the homology group $H_j [ C(n,p.q) ]$ is nontrivial. We prove three homology-vanishing theorems, based on discrete Morse theory on the cell complex. Then we describe several explicit families of nontrivial cycles, and a method for interpolating between parameters to fill in most of the picture for ``large-scale'' nontrivial homology.